Rarefied plasmas and their interactions with electromagnetic fields play an important role in many technological applications such as ion thrusters, ignition processes, electron and ion optics. Plasmas consist of freely moving electrons and ions, a state that requires a large amount of energy to achieve. This makes the experimental investigation of plasmas both difficult and expensive. Therefore, the ability to simulate plasma flows is very important as it provides easier access to understanding and analyzing complex phenomena.
For plasmas with a sufficiently high density, thermal equilibrium can be assumed, which usually leads to the use of methods that solve the magnetohydrodynamic equations. For lower densities, this assumption no longer applies. In these cases, the Boltzmann equation must be solved directly. This equation calculates the probability density function for each species within the phase space and describes the probability of a particle to have a certain position and velocity.
The PIC-DSMC solver PICLas approximates the probability density function using a large number of simulation particles. Since these particles are charged, they are accelerated by external electromagnetic fields and by electromagnetic fields generated by other charged particles. The temporal propagation of these fields is described by Maxwell's equations.
In many cases, the magnetic field induced by the movement of the particles can be neglected. This simplifies Maxwell's equations to the electro(quasi-)static equations. The interaction of the fields with the particles and vice versa is simulated using the Particle-In-Cell (PIC) method, in which the fields are calculated on a grid. The PIC method can be divided into four steps. First, the charge of the particles is distributed to the grid points by either assigning it to the nearest grid point or distributing it proportionally to nearby grid points. Next, the electric and magnetic fields are calculated using a suitable numerical method. In PIClas, high-order discontinuous Galerkin methods are used to calculate the fields. These high-order methods have the advantage that they require fewer grid points for the same accuracy compared to low-order methods. Thirdly, the forces acting on the particles are calculated. Once the fields are calculated, the solution on the grid points is interpolated to the particle positions. Finally, the particles are moved according to their velocity and accelerated by the force exerted by the fields. A common method for moving the particles is the leapfrog method, in which the position and velocity of the particles are stored at staggered times.
In current research, a major challenge in PIC simulations is the large difference in mass between electrons and ions. This means that the electrons have much higher velocities. While the main interest is usually on the motion of the ions, the motion of the electrons has to be resolved for stability reasons when using explicit methods. Therefore, research is currently focused on the exploration of implicit time integration methods that offer better stability properties.
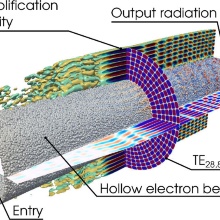
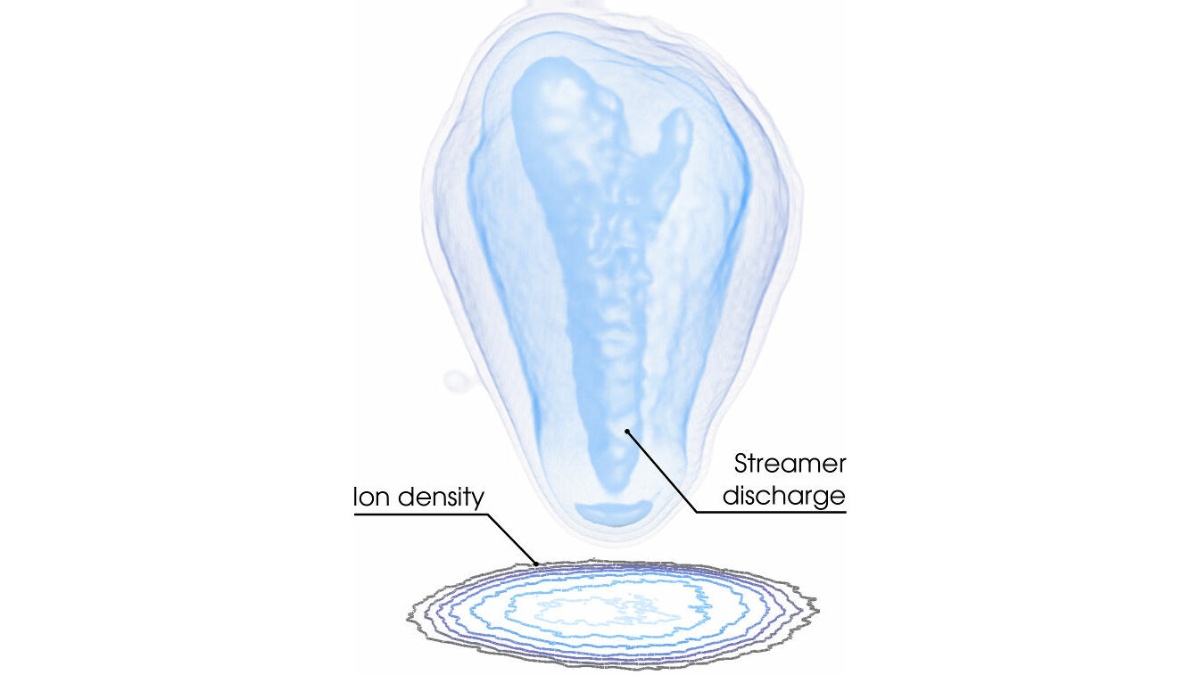
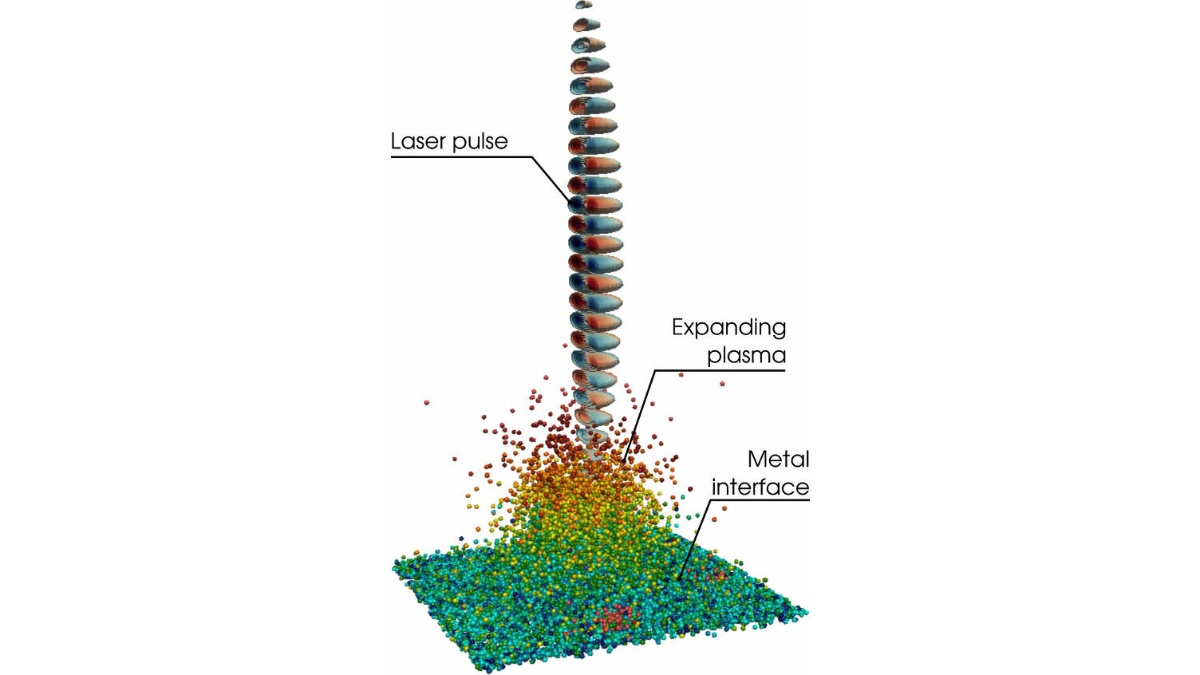
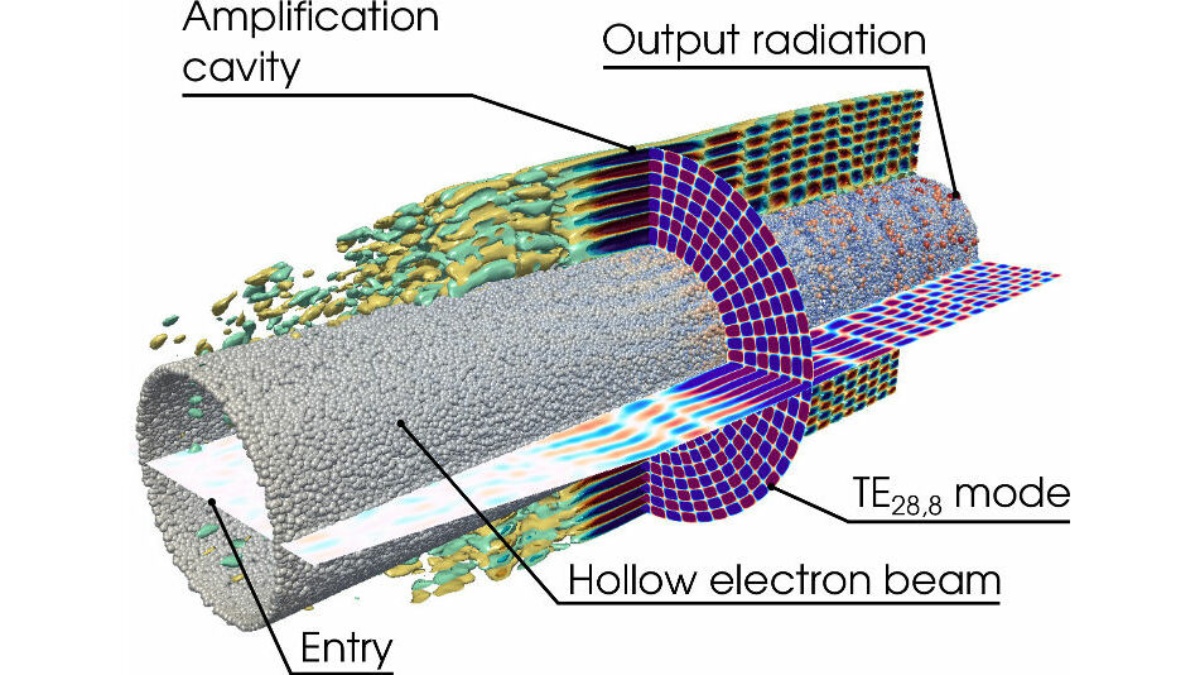
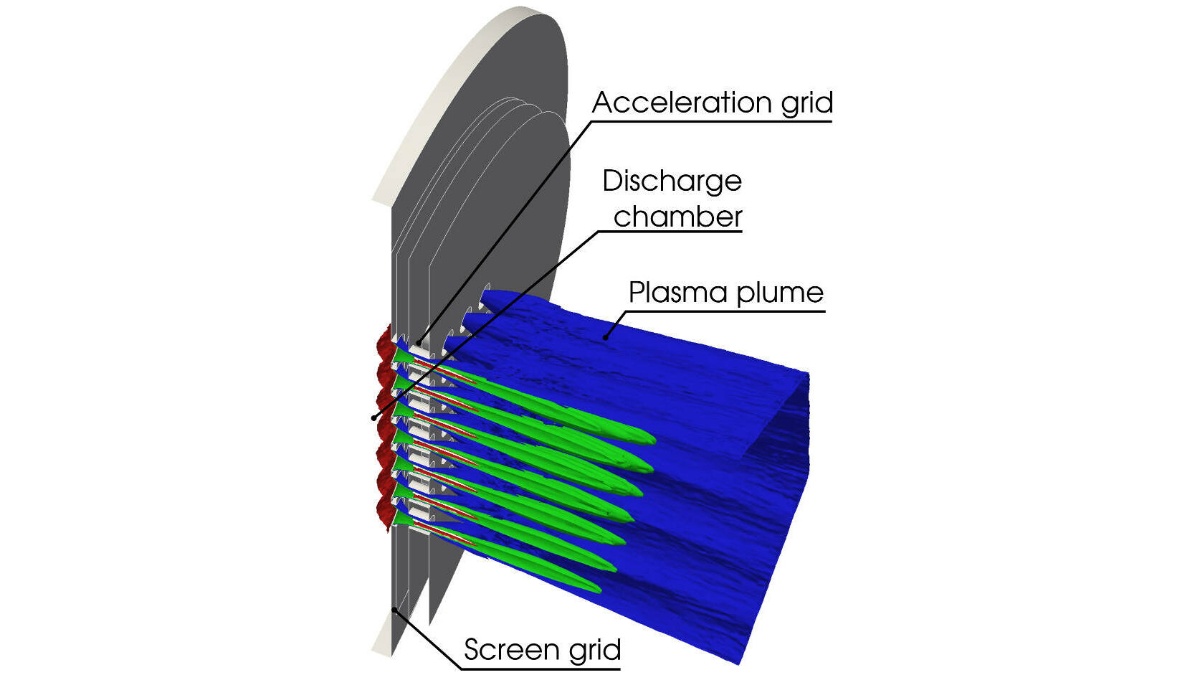
Various applications simulated with PICLas
Contact
Tobias Ott
M.Sc.Research Associate